طیفسنجی موزبائر اطلاعات ساختاری، مغناطیسی و الکترونیکی درون ماده را ارائه میدهد. در این روش هسته اولیه (چشمه)، پرتو گاما را گسیل کرده و هسته ثانویه (نمونه مورد مطالعه)، آن را با بازدهی خوبی جذب میکند. در طیفسنجی موزبائر هر دو هسته باید در یک بستر جامد محصور شوند که به این پدیده، اثر موزبائر گفته میشود. طیف موزبائر، شدت جذب پرتو گاما بر حسب انرژی هسته خاص رزونانسی 57Fe و یا 119Sn است.
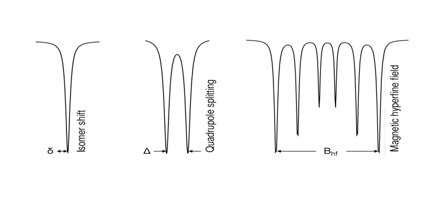
طیف موزبائر اطلاعات ساختاری را در مورد برهمکنشهای فوق‌ریزساختار نشان میدهد و شامل انرژی‌های کوچکی از برهمکنشهای بین هسته و الکترون‌های همسایه‌اش است. سه برهمکنش فوقریز شامل دانسیته الکترونی هسته‌ها (ایزومر شیفت)، تغییرات میدان الکتریکی (چهارقطبی الکتریکی) و دانسیته الکترون‌های جفت نشده (میدان مغناطیسی فوقریز) است.
یکی از پرکاربردترین موارد استفاده موزبائر در دنیا، در مطالعه مواد آمورف است که تقریبا کشف موزبائر با کشف مواد آمورف همزمان بوده است. مواد آمورف در حوزه‌های مختلف صنایع از جمله مواد مغناطیسی، پلیمر، فولاد، خوردگی و غیره کاربرد دارند. در این مقاله سعی شدهاست تا اصول و چگونگی کار دستگاه طیفسنجی موزبائر مورد بررسی قرار گرفته و به طور گسترده در مورد مواد آمورف و تحلیل طیف‌های موزبائر در حوزه خواص مغناطیسی و ساختارهای فازی آنها بحث شود.
این مقاله شامل سرفصل‌های زیر است:
1- مقدمه
2- اصول طیفسنجی موزبائر
3- کسر بدون پسزنی
4- مولفه‌های طیف موزبائر
1-4- ایزومر شیفت(
)
2-4- برهمکنش چهار قطبی الکتریکی Δ
3-4- برهمکنش دوقطبی مغناطیسی فوق ریزساختار
5- شبکه آزمایشگاهی فناوری راهبردی
1- مقدمه
2- اصول طیفسنجی موزبائر
3- کسر بدون پسزنی
4- مولفه‌های طیف موزبائر
1-4- ایزومر شیفت(
)2-4- برهمکنش چهار قطبی الکتریکی Δ
3-4- برهمکنش دوقطبی مغناطیسی فوق ریزساختار
5- شبکه آزمایشگاهی فناوری راهبردی
1- مقدمه
در سال 1958 رادولوف موزبائر پدیده‌ای را کشف کرد که امروزه از آن به عنوان «اثر موزبائر» یاد میشود. او برای انجام تز دکترای خود با عنوان «اندازه‌گیری پراکندگی رزونانس هستهای در عنصر 191Ir توانست به این کشف بسیار بزرگ که از دقت فوق‌العاده بالایی برخوردار است، دست یابد. داده‌های به‌دست آمده از این آنالیز دارای دقتی معادل 1 بر 1012 است؛ یعنی مقیاس یک ورق کاغذ در فاصله بین زمین و خورشید. به همین دلیل این روش قادر به شناسایی برهمکنشهای فوقریز ساختار در ابعاد هستهای است. این روش به چگونگی آرایش اتم‌های احاطه شده و ساختار بلوری محلی و محیط‌های شیمیایی و ساختاری، بسیار حساس است و اطلاعات ارزشمندی را در مورد ساختار و خصوصیات مغناطیسی و الکترونیکی مواد (مثل الکترووالانس، حالت اسپینی و اندازه حرکت) ارائه میدهد. همچنین طیفسنجی موزبائر برای آنالیزهای فازی کمی با توجه به میزان تمرکز عناصر رزونانسی در فازهای مختلف نانوساختار و یا آمورف، کاربرد دارد. با وجود اینکه برهمکنشهای فوقریز به راحتی قابل تحلیل نیستند، اما به مثابه «اثر انگشت» در تشخیص اختلافات محیطی از نظر شیمیایی در اتم رزونانس، معتبراند و با توجه به درصد فراوانی فازها، با اطمینان بالایی قابل تحلیل و بررسی هستند. طیفسنجی موزبائر در بسیاری از حوزه‌های علمی و صنعتی دنیا کاربرد دارد و به دلیل قابلیت‌های منحصر به فرد، به روش متداول آنالیزی در دنیا تبدیل شدهاست؛ به طوری که تعداد مقالات چاپ شده در این حوزه از مرز 60000 گذشته است. نتایج چشمگیر و قابل توجه این آنالیز در حوزه‌های فیزیک، مغناطیس، مهندسی مواد و متالورژی، مطالعه ساختارهای الکترونی مواد، علم سطح، شیمی، کاتالیست‌ها، صنعت فولاد، مطالعات خوردگی، مکانیک سیالات، بیوتکنولوژی و پزشکی، کشاورزی، محیط‌‌‌زیست، زمین‌شناسی و کانی‌شناسی، مطالعات اکتشافات فضایی و باستان‌شناسی گزارش شدهاست که نشان‌دهنده ارتباط تنگاتنگ این روش با تحقیقات علمی روز دنیا است.
2- اصول طیفسنجی موزبائر
طیفسنجی موزبائر بر اصول مکانیک کوانتومی استوار است و ارتباط ناگسستنی بین فیزیک حالت جامد و هستهای دارد. این روش، گذار بین حالات هستهای را اندازه‌گیری و بررسی میکند. غالب ویژگی‌های هسته اتم و مواد هستهای معلوم شدهاست اما بیشتر این ویژگی‌ها و به تبع آن، کاربردهای آنها توسط متخصصین حوزه‌های مختلف به خوبی شناخته نشده‌است. از آنجا که طیفسنجی موزبائر گذار حالات هستهای را اندازه‌گیری میکند، لازم است که ویژگی‌های هسته در ماده به خوبی درک و شناخته شود. به همین دلیل بحث را با مروری بر دانش کوانتومی و هستهای آغاز میکنیم. در هسته، گذارهایی بین حالات کوانتومی، مثل الکترون‌ها و اتم‌ها روی میدهد که باعث تغییرات بزرگی در انرژی میشود. هر هسته را با مشخصه‌های کوانتومی E, I, Iz توصیف میکنند که E انرژی، I اسپین هسته و Iz اسپین هسته در جهت z است. از طرفی باید بدانیم که مختصات فضایی X ، به عنوان مرکز جرم هسته برای فهمیدن ارتعاشات هستهای در فضا و یا شبکه بلوری ضروری است. سیستم مختصات داخلی هسته به هم وابسته هستند. برای مثال، اولین حالت برانگیخته هسته اتم ،57Fe دارای اسپین I = 3/ 2 است که به دلیل قواعد کوانتومی دارای چهار مقدار مجاز Iz است: 1/2 ، 3/2 ، 1/2- ، 3/2-
اسپین حالت پایه اتم 57Fe ، یک دوم (1/2) است که دو مقدار مجاز 1/2 و 1/2- دارد. در غیاب برهمکنشهای فوقریز، همه سطوح انرژی و کلیه گذارهای مجاز بین ترازهای اسپینی در یک سطح انرژی مشابه روی میدهد و سطح مقطع کل هسته جاذب °σ ، است. توجه داشته باشید اگرچه سطح مقطع فوق، تقریبا 100 برابر کوچکتر از یک سطح مورد هدف در مورد یک ابر الکترونی اتمی است، اما صدها برابر بزرگتر از سطح مقطع تفرق یک فوتون با انرژی 14/4KeV از الکترون‌های اتمی 57Fe است.
طول عمر، مشخصه حالت برانگیخته هسته اتم τ = 141 ns ،57Fe است که نسبت به عناصر دیگر، دارای بازه زمانی طولانی‌تری است. به طور کلی در تابش‌های سنکروترونی، هسته‌های مستقل اتم 57Fe در حالت برانگیخته، به طور همزمان میتوانند با طول عمرهای مختلف τ واپاشی داشته باشند. احتمال واپاشی هسته اتم 57Fe در واحد زمان به شکل زیر است:
اسپین حالت پایه اتم 57Fe ، یک دوم (1/2) است که دو مقدار مجاز 1/2 و 1/2- دارد. در غیاب برهمکنشهای فوقریز، همه سطوح انرژی و کلیه گذارهای مجاز بین ترازهای اسپینی در یک سطح انرژی مشابه روی میدهد و سطح مقطع کل هسته جاذب °σ ،
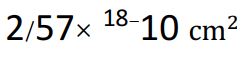است. توجه داشته باشید اگرچه سطح مقطع فوق، تقریبا 100 برابر کوچکتر از یک سطح مورد هدف در مورد یک ابر الکترونی اتمی است، اما صدها برابر بزرگتر از سطح مقطع تفرق یک فوتون با انرژی 14/4KeV از الکترون‌های اتمی 57Fe است.طول عمر، مشخصه حالت برانگیخته هسته اتم τ = 141 ns ،57Fe است که نسبت به عناصر دیگر، دارای بازه زمانی طولانی‌تری است. به طور کلی در تابش‌های سنکروترونی، هسته‌های مستقل اتم 57Fe در حالت برانگیخته، به طور همزمان میتوانند با طول عمرهای مختلف τ واپاشی داشته باشند. احتمال واپاشی هسته اتم 57Fe در واحد زمان به شکل زیر است:
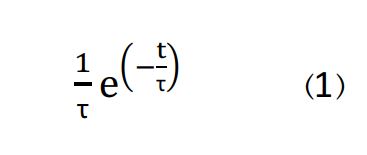
با توجه به اصل عدم قطعیت کوانتومی هایزنبرگ، مدت زمان حالت برانگیخته هستهای τ، به عدم قطعیت انرژی حالت برانگیخته ∆E، با فرمول h~∆E. τ وابسته است. که برای τ = 141 ns، عدم قطعیت در انرژی معادل 
خواهد بود.
در یک گذار ساده درون هسته، وابستگی انرژی به سطح مقطع در تفرق موزبائر به شکل تابع لورنتسی است که پهنای آن با استفاده از پهنشدگی انرژی حالت برانگیخته هسته تعریف میشود که در مورد 57Fe این پهنا
است. اما هنگامی که ترازهای انرژی برانگیخته شده هسته‌های متفاوت موزبائر یکسان نباشند و تفرق‌ها در هسته مستقل از هم عمل کنند، سطح مقطع کل به شکل زیر خواهد بود
خواهد بود.در یک گذار ساده درون هسته، وابستگی انرژی به سطح مقطع در تفرق موزبائر به شکل تابع لورنتسی است که پهنای آن با استفاده از پهنشدگی انرژی حالت برانگیخته هسته تعریف میشود که در مورد 57Fe این پهنا
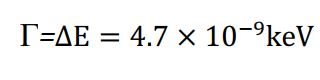است. اما هنگامی که ترازهای انرژی برانگیخته شده هسته‌های متفاوت موزبائر یکسان نباشند و تفرق‌ها در هسته مستقل از هم عمل کنند، سطح مقطع کل به شکل زیر خواهد بود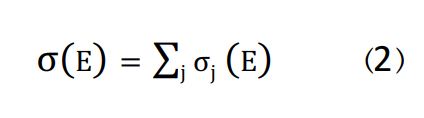
اصول کلی طراحی طیفسنجی موزبائر معمولا بر اساس محاسبه وابستگی انرژی به سطح مقطع کل σ(E) انجام میشود که مجموع توابع لورنتسی از پهنای طبیعی خط Γ است. بر این اساس، اکنون در نظر میگیریم که هسته‌های ثانویه با جذب انرژی پرتو گاما از هسته اولیه برانگیخته میشوند که دقت انرژی حالت برانگیخته هستهای از درجه 8-10 الکترون ولت است. در دمای اتاق، ارتعاشات مرکز جرم هسته دارای انرژی eV/atom 2/5*2-10 است. در صورتیکه تغییرات انرژی ارتعاشی هسته در طول گسیل پرتو گاما روی دهد، این مقدار انرژی پرتو گاما برای وقوع پدیده جذب رزونانس قوی هسته ثانویه، بسیار نامناسب و غیردقیق است.
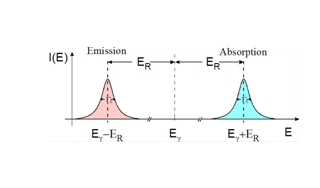
هر گسیل پرتو گاما از هسته با جرم m با ممنتوم Eγ/c=Py با پسزنی از سوی سیستم گسیلنده با ممنتومی در خلاف جهت خود همراه است. در این وضعیت، جرم اولیه m دارای انرژی پسزنی ER است که همین مقدار از انرژی پرتو گاما اولیه کاسته شده و به سمت جرم دوم ′ m حرکت میکند. انرژی پسزنی با استفاده از فرمول زیر به‌دست می‌آید:
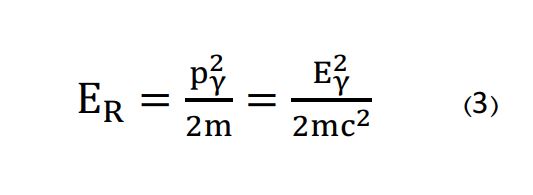
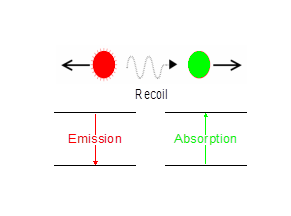
در مورد جرم 57Fe با گسیل پرتو گاما، دارای مقدار انرژی پسزنی 3-10*1/86 ev میشود که این مقدار انرژی، بسیار بزرگتر از دقت انرژی مورد نیاز برای جذب پرتو گاما توسط هسته ثانویه است. تز دکترای رادولف موزبائر اندازه‌گیری رزونانس هستهای در عنصر ایریدیوم 119 بود. او برای این کار، از پهنای دوپلر حرارتی خطوط گسیلی برای جبران انرژی از دست رفته پسزنی استفاده کرد. او انتظار داشت با این روش، تعداد جذب هستهای رزونانسی بسیار کم باشد اما برخلاف انتظار وی تعداد آنها زیاد بود و وقتی که چشمه و جاذب تحت دمای نیتروژن مایع سرد شدند، این آمار جذب بالاتر هم رفت. وی همچنین توانست روشی را برای ایجاد طیفی از پرتو گاما به‌دست آورد که بتواند در ایجاد رزونانس مفید و موثر باشد. او برای این کار، از خاصیت دوپلر استفاده کرد. رابطه بین انرژی گامای دریافتی و سرعت حرکت چشمه نسبت به نمونه به صورت 
است. شکل (4) نمایی از این تغییر را نشان میدهد.
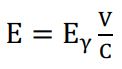است. شکل (4) نمایی از این تغییر را نشان میدهد.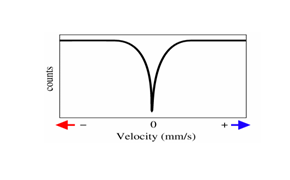
برای حل مشکل، موزبائر کشف کرد که در شرایطی، جرم m را میتوان مساوی جرم کل بلور دانست. با این فرض که جرم هسته محکم به جرم بلور متصل است. این موضوع درست مثل یک نوسانگر هارمونیک ساده با انرژی کوانتیزه است که هسته‌های 57Fe با استفاده از یک فنر به جرم کل بلور پیوند دارند. در این حالت، انرژی پسزنی به دست آمده از معادله شماره (3)، بسیار کوچک شده، انرژی پرتو گامای خروجی دارای دقتی بسیار بیشتر از 9-10 الکترون ولت خواهد شد که توسط هسته ثانویه جذب میشود. با در نظر گرفتن کل شبکه به صورت جرم واحد، ارتعاشات شبکه به قدری کم است که تقریبا احتمال برانگیختگی فونون‌ها در حین گسیل پرتو گاما وجود ندارد. زیرا در صورت وجود ارتعاشات شبکه، انرژی برانگیختگی فونون‌ها از درجه 2-10 است که وجود هرگونه رزونانس را از بین میبرد.
3- کسر بدون پسزنی
با استفاده از محاسبات کوانتومی، برای هر هستهای میتوان میزان پسزنی هسته را بررسی کرد. در مکانیک کوانتوم، کمیت f به عنوان کسر بدون پسزنی تعریف میشود و احتمال این را میدهد که بعد از گسیل پرتو گاما با ممنتوم pγ از مرکز جرم هسته، تغییری در تابع حالت شبکه مرکز جرم هسته ایجاد نشود. به عبارت دیگر، f احتمال گسیل پرتو گاما را بدون افت انرژی به سمت فونون‌ها (ذرات حامل انرژی در شبکه بلوری) بررسی میکند و البته مشابه همین عامل برای جذب پرتو گاما توسط هسته ثانویه نیز به کار می‌رود. محاسبه f از طریق فرمول زیر انجام میشود:
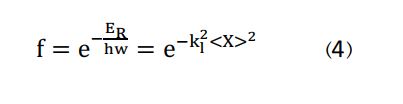
که در آن متوسط مربع جابجایی هسته‌های محصور در نوسانگر است. شرط به‌دست آوردن تعداد معناداری از گسیل پرتو گاما بدون پسزنی این است که مشخصه انرژی پسزنی هسته‌های آزاد، ER کوچکتر و یا هم مرتبه انرژی فونون‌ها با طول موج کوتاه در شبکه باشد. انرژی فونون‌ها از طریق دمای دبای و یا دمای اینشتین، چند ده‌میلی الکترون ولت و انرژی پسزنی ER در 57Fe ، 
است که مشاهده می‌کنید این دو مقدار هم‌مرتبه یکدیگر هستند. ما وارد جزئیات بحث فوق نخواهیم شد چون محاسبه آن بسیار پیچیده است.
عامل قابل مشاهده در اثر موزبائر، شدت طیف است که در معادله (4) قابل بررسی است. فاکتور بدون پسزنی به مثابه فاکتور دبای- والر در پراش پرتو X است. این فاکتور، زمانی که شبکه بلوری نرم است و ωE بزرگ شود، بیشتر میشود. همچنین این عامل، متوسط وزنی روی همه فونون‌های یک شبکه بلوری محاسبه میشود. در محاسبه همین عامل، نکات بسیار ظریفی وجود دارد که خارج از هدف این مبحث است. راه معمول برای محاسبه فاکتور بدون پسزنی یک ماده تک فاز، محاسبه مساحت طیف موزبائر برحسب دما است. همانطور که در معادله (4) ملاحظه می‌کنید شدت اثر موزبائر با افزایش متوسط مربع جابجایی 2 کاهش می‌یابد. کمیت با افزایش دما بیشتر شده و از این رو محاسبه شدت طیف بر حسب دما برای تعیین فاکتور بدون پسزنی f و همچنین دمای دبای و اینشتین لازم است. این عوامل لزوم اهمیت در آماده‌سازی و مدت زمان آنالیز یک مجموعه از نمونه‌ها را ضروری میکند. از طرفی لازم به ذکر است که در موزبائر به دلیل قابل اغماض بودن ارتعاشات شبکه و پهنشدگی دوپلر حرارتی، پهنشدگی خطوط جذب را میتوان به دلیل برانگیخته شدن هسته اتم دانست. به همین دلیل، عوامل قابل حصول در موزبائر ناشی از تغییرات در هسته اتم است.
است که مشاهده می‌کنید این دو مقدار هم‌مرتبه یکدیگر هستند. ما وارد جزئیات بحث فوق نخواهیم شد چون محاسبه آن بسیار پیچیده است.عامل قابل مشاهده در اثر موزبائر، شدت طیف است که در معادله (4) قابل بررسی است. فاکتور بدون پسزنی به مثابه فاکتور دبای- والر در پراش پرتو X است. این فاکتور، زمانی که شبکه بلوری نرم است و ωE بزرگ شود، بیشتر میشود. همچنین این عامل، متوسط وزنی روی همه فونون‌های یک شبکه بلوری محاسبه میشود. در محاسبه همین عامل، نکات بسیار ظریفی وجود دارد که خارج از هدف این مبحث است. راه معمول برای محاسبه فاکتور بدون پسزنی یک ماده تک فاز، محاسبه مساحت طیف موزبائر برحسب دما است. همانطور که در معادله (4) ملاحظه می‌کنید شدت اثر موزبائر با افزایش متوسط مربع جابجایی 2 کاهش می‌یابد. کمیت با افزایش دما بیشتر شده و از این رو محاسبه شدت طیف بر حسب دما برای تعیین فاکتور بدون پسزنی f و همچنین دمای دبای و اینشتین لازم است. این عوامل لزوم اهمیت در آماده‌سازی و مدت زمان آنالیز یک مجموعه از نمونه‌ها را ضروری میکند. از طرفی لازم به ذکر است که در موزبائر به دلیل قابل اغماض بودن ارتعاشات شبکه و پهنشدگی دوپلر حرارتی، پهنشدگی خطوط جذب را میتوان به دلیل برانگیخته شدن هسته اتم دانست. به همین دلیل، عوامل قابل حصول در موزبائر ناشی از تغییرات در هسته اتم است.
4- مولفه‌های طیف موزبائر
طیفسنجی موزبائر، طیفی از انرژی‌های مرتبط با هسته جاذب گاما را اندازه میگیرد. در حال حاضر این روش با هسته‌های 57Co, 119Sn, 151Eu, 121Sb, 162Dy انجام میشود که البته 57Co در بین این عناصر، کاربردیترین و معمولترین آنها است. مهمترین کاربرد طیفسنجی موزبائر، استفاده از عوامل فوقریز ساختار است که الکترون‌های اطراف هسته باعث ایجاد افت و خیز انرژی در ترازهای هسته میشوند. این برهمکنشهای فوقریز دارای انرژی بسیار کوچک و از مرتبه 7-10 تا 9-10 الکترون ولت است، در حالی که انرژی پرتو گاما دارای انرژی از مرتبه 104 تا 105 الکترون ولت است. با مقایسه انرژی برهمکنشهای ریز با انرژی پرتو گاما میتوان متوجه شد که دقت روش موزبائر از مرتبه 1012 است. در موزبائر با رفع موانعی که در بخش‌های قبلی توضیح داده شد، افت و خیز‌های برهمکنشهای فوقریز به راحتی و با دقت بالا و هزینه کم، قابل اندازه‌گیری هستند.
برهمکنشهای الکترون- هسته اولین بار در طیف‌های نوری به صورت شکافتگی‌های ضعیفتر از آنچه که در برهمکنشهای ریز الکترون- الکترون مشاهده شده بود، دیده شد. برهمکنشهای فوقریز، برخاسته از دانسیته الکترون‌ها در هسته‌ها، تغییرات میدان الکتریکی و یا اسپین‌های الکترونی جفت نشده در هسته‌ها است که به ترتیب آنها را با ایزومر شیفت، برهمکنش چهار قطبی الکتریکی و برهمکنش دوقطبی مغناطیسی فوق ریزساختار میشناسند.
برهمکنشهای الکترون- هسته اولین بار در طیف‌های نوری به صورت شکافتگی‌های ضعیفتر از آنچه که در برهمکنشهای ریز الکترون- الکترون مشاهده شده بود، دیده شد. برهمکنشهای فوقریز، برخاسته از دانسیته الکترون‌ها در هسته‌ها، تغییرات میدان الکتریکی و یا اسپین‌های الکترونی جفت نشده در هسته‌ها است که به ترتیب آنها را با ایزومر شیفت، برهمکنش چهار قطبی الکتریکی و برهمکنش دوقطبی مغناطیسی فوق ریزساختار میشناسند.
1-4- ایزومر شیفت():
برهمکنش کولنی توزیع بار-هسته در یک هسته با ابعاد مشخص R، منشا ایجاد ایزومر شیفت در حالت‌های پایه و برانگیخته و دانسیته بار- الکترون در هسته (الکترون s) است. در برهمکنش کولنی، فرض بر این است که الکترون‌ها حول هسته در یک فاصله زیاد از هسته در حال دوران هستند و میتوان هسته را به عنوان یک بار نقطهای در نظر گرفت. اما در واقع، هسته‌ها دارای یک اندازه مشخص و با شعاع تقریبی زیر هستند:
در حالت‌های پایه و برانگیخته و دانسیته بار- الکترون در هسته (الکترون s) است. در برهمکنش کولنی، فرض بر این است که الکترون‌ها حول هسته در یک فاصله زیاد از هسته در حال دوران هستند و میتوان هسته را به عنوان یک بار نقطهای در نظر گرفت. اما در واقع، هسته‌ها دارای یک اندازه مشخص و با شعاع تقریبی زیر هستند: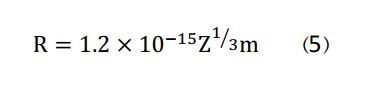
که در آن Z عدد اتمی هسته است. در حالی که قسمت اعظم دانسیته بار الکترونی در یک فاصله مشخص از هسته قرار دارد، موضوع نوع پیوندهای الکترونی در شیمی در دیگر تجهیزات طیفسنجی، قابل بحث و بررسی است. اما الکترون‌های s,p یک دوم (1/2) با احتمال کوچک مشخصی میتوانند در هسته حضور داشته باشند. این اثر در الکترون‌های s بیشتر دیده میشود که موجب تغییرات انرژی کل، در سطوح هستهای میشود.
اثر فوق به دلیل اینکه مقدارش از حد توانایی و قدرت تفکیک و پیش‌بینی‌های تئوری کوچکتر است، قابل مشاهده نیست. البته در بحث گسیل پرتو گاما، هسته‌ها، گذارهایی را از حالت برانگیخته به حالت پایینتر خواهند داشت که باعث تغییر شعاع هسته در دو حالت پایه و برانگیخته میشود. میزان برهمکنش‌ها، حاصل از انتگرال دانسیته بار الکترونی و بار هسته در فضای تداخلی آنها است. چون حجم ناحیه تداخلی در هر دو حالت با هم فرق دارند، پس ناحیه تداخلی در هسته نیز تغییر میکند. محاسبه اولین ایزومر شیفت توسط کیستنر و سانیار در سال 1960 و اولین تحلیل سیستماتیک در مورد ایزومر شیفت توسط والر.ات.آل در سال 1961 صورت گرفت. توصیف ریاضی ایزومر شیفت، به شکل زیر است:
اثر فوق به دلیل اینکه مقدارش از حد توانایی و قدرت تفکیک و پیش‌بینی‌های تئوری کوچکتر است، قابل مشاهده نیست. البته در بحث گسیل پرتو گاما، هسته‌ها، گذارهایی را از حالت برانگیخته به حالت پایینتر خواهند داشت که باعث تغییر شعاع هسته در دو حالت پایه و برانگیخته میشود. میزان برهمکنش‌ها، حاصل از انتگرال دانسیته بار الکترونی و بار هسته در فضای تداخلی آنها است. چون حجم ناحیه تداخلی در هر دو حالت با هم فرق دارند، پس ناحیه تداخلی در هسته نیز تغییر میکند. محاسبه اولین ایزومر شیفت توسط کیستنر و سانیار در سال 1960 و اولین تحلیل سیستماتیک در مورد ایزومر شیفت توسط والر.ات.آل در سال 1961 صورت گرفت. توصیف ریاضی ایزومر شیفت
، به شکل زیر است: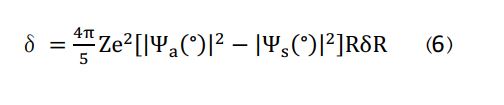
که در آن 
دانسیته نسبی الکترون در هسته با شعاع صفر است؛ اندیس a مربوط به جاذب و اندیس s برای چشمه و همچنین ضخامت پوسته است. از آنجایی که تغییر دانسیته الکترونی در هسته تابعی از الکترون والانس و پیوندهای شیمیایی است؛ به ایزومر شیفت، عنوان «شیفت شیمیایی» هم داده شدهاست. از روی جهت شیفت خطوط رزونانس، با افزایش دانسیته الکترون‌های s، 
دارای علامت منفی در 57Fe بوده و به این معناست که شعاع هستهای در حالت برانگیخته، کوچکتر از شعاع در حالت پایه است که این نتیجه در مورد ایزوتوپ 119Sn برعکس است. ایزومر شیفت فلزات با اثرات پوشش بسیار بیشتر تغییر میکنند. ایزومر شیفت ،57Fe متناسب با تغییر حالت بارهای آهن، گواهی از تاثیر این اثر پوششی است و تحلیل آن عمدتا بر اساس دو سهم عمده الکترون‌های s4 و d3 با مشخصه‌های مناسب انجام میشود.
دانسیته نسبی الکترون در هسته با شعاع صفر است؛ اندیس a مربوط به جاذب و اندیس s برای چشمه و همچنین ضخامت پوسته است. از آنجایی که تغییر دانسیته الکترونی در هسته تابعی از الکترون والانس و پیوندهای شیمیایی است؛ به ایزومر شیفت، عنوان «شیفت شیمیایی» هم داده شدهاست. از روی جهت شیفت خطوط رزونانس، با افزایش دانسیته الکترون‌های s، 
دارای علامت منفی در 57Fe بوده و به این معناست که شعاع هستهای در حالت برانگیخته، کوچکتر از شعاع در حالت پایه است که این نتیجه در مورد ایزوتوپ 119Sn برعکس است. ایزومر شیفت فلزات با اثرات پوشش بسیار بیشتر تغییر میکنند. ایزومر شیفت ،57Fe متناسب با تغییر حالت بارهای آهن، گواهی از تاثیر این اثر پوششی است و تحلیل آن عمدتا بر اساس دو سهم عمده الکترون‌های s4 و d3 با مشخصه‌های مناسب انجام میشود.
2-4- برهمکنش چهار قطبی الکتریکی Δ:
در بخش قبل فرض بر این بود که هسته‌ها چه در حالت پایه و چه در حالت کروی دارای ساختار کروی هستند. اما باید به این نکته نیز توجه داشت که در واقعیت، هر هسته با داشتن ممنتوم زوایه‌ای بزرگتر از 1/2 دارای شکل غیرکروی است. محاسبه میزان انحراف هسته از شکل کروی را ممنتوم چهارقطبی هستهای الکتریکی گویند که با فرمول زیر تعریف میشود:
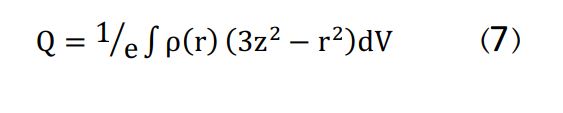
توصیف مناسب از میدان بلوری بیضوی، از طریق محاسبه مشتق دوم پتانسیل الکتریکی، یا به عبارتی گرادیان میدان الکتریکی EFG، انجام میشود. هر شکل فیزیکی معنادار در مرتبه دوم، با یک مجموعه از محورهای مختصات اورتوگنال قابل تعریف است و میتوان EFG را بر حسب آنها توصیف نمود:
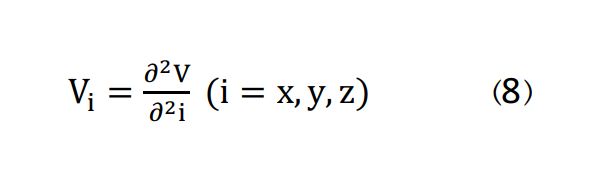
از آنجا که پتانسیل الکتروستاتیکی با استفاده از معادله لاپلاس قابل محاسبه است و با توجه به آن فقط دو عامل از سه عامل مستقل هستند، فاکتور نامتقارنی 
هسته با فرمول زیر تعریف میشود:
هسته با فرمول زیر تعریف میشود:
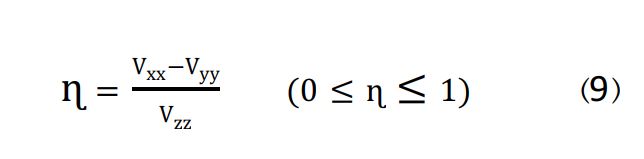
در این نوع برهمکنش که بین گرادیان میدان الکتریکی EFG و میدان الکتریکی چهارقطبی الکتریکی هسته اتفاق میافتد، ترازهای هسته شکافته میشوند و در آنها شکافتگی سطوح انرژی به صورت 2l+1 روی میدهد (I + ml⟩, I − ml) که در آن شکافتگی خطوط به شکل زیر خواهد بود:
شکافتگی خطوط برای اولین بار توسط کیستنر و سانیار در سال 1960 مشاهده شد. عامل شکافتگی چهارقطبی به تعیین ساختار محلی کمک میکند و به تقارن نقطهای محیط اتم‌های مورد بررسی بسیار حساس است.
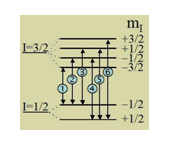
3-4- برهمکنش دوقطبی مغناطیسی فوق ریزساختار:
از آنجایی که پروتون و نوترون دارای دوقطبی مغناطیسی است، همه هسته‌ها نیز دارای ممنتوم دوقطبی مغناطیسی هستند، البته به جز آنهایی که دارای تعداد پروتون و نوترون زوج هستند؛ چون مقدار ممنتوم زاویه‌ای کل I آنها در حالت پایه صفر است. هسته‌ها در حالت‌های برانگیخته دارای ممنتوم مغناطیسی غیرصفر هستند. ممنتوم مغناطیسی هستهای با ممنتوم مغناطیسی الکترون‌ها برهمکنش داده و برهمکنش مغناطیسی فوقریز ساختار را تشکیل میدهند. اولین مشاهده شکافتگی فوقریز ساختار مغناطیسی با استفاده از طیفسنجی موزبائر 57Fe، توسط پوند و ربکا در سال 1959 صورت گرفت. برهمکنش ممنتوم دوقطبی مغناطیسی هستهای μ با میدان مغناطیسی H، در محل هسته‌ها، باعث شکافتگی حالت هستهای با اسپین به 2l+1 زیر تراز میشود. انرژی دژنره با معادله زیر تعریف میشود:
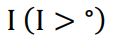به 2l+1 زیر تراز میشود. انرژی دژنره با معادله زیر تعریف میشود: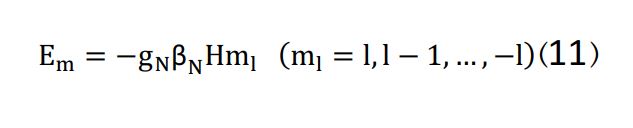
که در آن ml عدد کوانتومی مغناطیسی است. ممنتوم مغناطیسی هسته با مگنتون هستهای بوهر βN و با فاکتور شکافتگی لانداو هستهای مرتبط است:
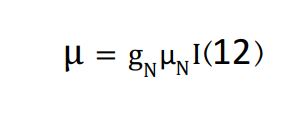
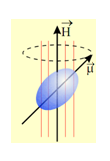
این شکافتگی‌ها باعث میشود که طیف اولیه به تعداد زیادی خطوط شکافته شود و تعداد این خطوط به مقدار Iدر حالت‌های پایه و برانگیخته بستگی دارد. ایزوتوپ 57Fe در حالت پایه‌اش دارای مقدار ممنتوم زاویه‌ای 1/2 و مقدار آن در اولین حالت برانگیخته، 3/2 است. میزان شکافتگی مغناطیسی هسته‌ها، مستقیما به میدان مغناطیسی هسته که عمدتا به آن میدان موثر درونی Hef گفته میشود، بستگی دارد. برهمکنش فوقریز مغناطیسی به‌دست آمده از موزبائر، نقش مهمی را در فهمیدن خصوصیات مغناطیسی مواد دارد. مثلا در ترکیبات فریتی و آلیاژها هر مکانی در شبکه، در الگوی فوقریز دیده میشود که با این روش میتوان رفتار زیرشبکه‌ها و ناخالصی‌ها را مطالعه کرد.
5- شبکه آزمایشگاهی فناوری راهبردی
این مقاله از مجموعه مقالات فصل نامه شبکه آزمایشگاهی فناوری‌های راهبردی سال 2013، شماره 3 برگرفته شده است. برای دسترسی به مراکز خدمات دهنده آنالیز دستگاه طیفسنجی موزبائر بر روی لینک زیر کلیک کنید.
| نام دستگاه |
| طیفسنجی موزبائر |
منابـــع و مراجــــع
۱ – Mossbauer Spectroscopy of Environmental Materialstheir Industrial Utilization (Enver Muard & John Cashion)
۲ – Topics in Applied Physics (U.Gonser)
۳ – Mossbauer Spectromety (Brent Fultz, Department of Applied physicsMaterial Science)Microscopic methods in metals (U.Gonser)Industrial Applications of the Mossbauer Effect (Desmond C.CookGilbert R.Hoy)
۴ – Mossbauer SpectroscopyTransition Metal Chemistry (Philipp Gutlich Eckhard Bill, Alfred X.Trautwein)
۵ – فصل نامه شبکه آزمایشگاهی فناوری‌های راهبردی سال 2013 و شماره 3
